Code
knitr::opts_chunk$set(echo = TRUE)Kaushika Potluri
August 2, 2022
# A tibble: 725 × 6
LungCap Age Height Smoke Gender Caesarean
<dbl> <dbl> <dbl> <chr> <chr> <chr>
1 6.48 6 62.1 no male no
2 10.1 18 74.7 yes female no
3 9.55 16 69.7 no female yes
4 11.1 14 71 no male no
5 4.8 5 56.9 no male no
6 6.22 11 58.7 no female no
7 4.95 8 63.3 no male yes
8 7.32 11 70.4 no male no
9 8.88 15 70.5 no male no
10 6.8 11 59.2 no male no
# … with 715 more rowsThe distribution appears to be very similar to a normal distribution, according to the histogram.
The boxplots below show the probability distributions grouped by Gender.
Looks like males have a slightly higher lung capacity than females.
# A tibble: 2 × 2
Smoke Mean
<chr> <dbl>
1 no 7.77
2 yes 8.65Surprisingly, the mean lung capacity is higher for smokers than it is for non-smokers.
# A tibble: 725 × 7
LungCap Age Height Smoke Gender Caesarean AgeGroup
<dbl> <dbl> <dbl> <chr> <chr> <chr> <chr>
1 5.88 3 55.9 no male no 13 and lower
2 0.507 3 51.6 no female yes 13 and lower
3 1.18 3 51.9 no male no 13 and lower
4 4.7 3 52.7 no male no 13 and lower
5 5.48 3 52.9 no male no 13 and lower
6 1.02 3 47 no female no 13 and lower
7 2 3 51 no female no 13 and lower
8 1.68 3 51.9 no male no 13 and lower
9 4.08 3 53.6 no male yes 13 and lower
10 1.45 3 45.3 no female no 13 and lower
# … with 715 more rows`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.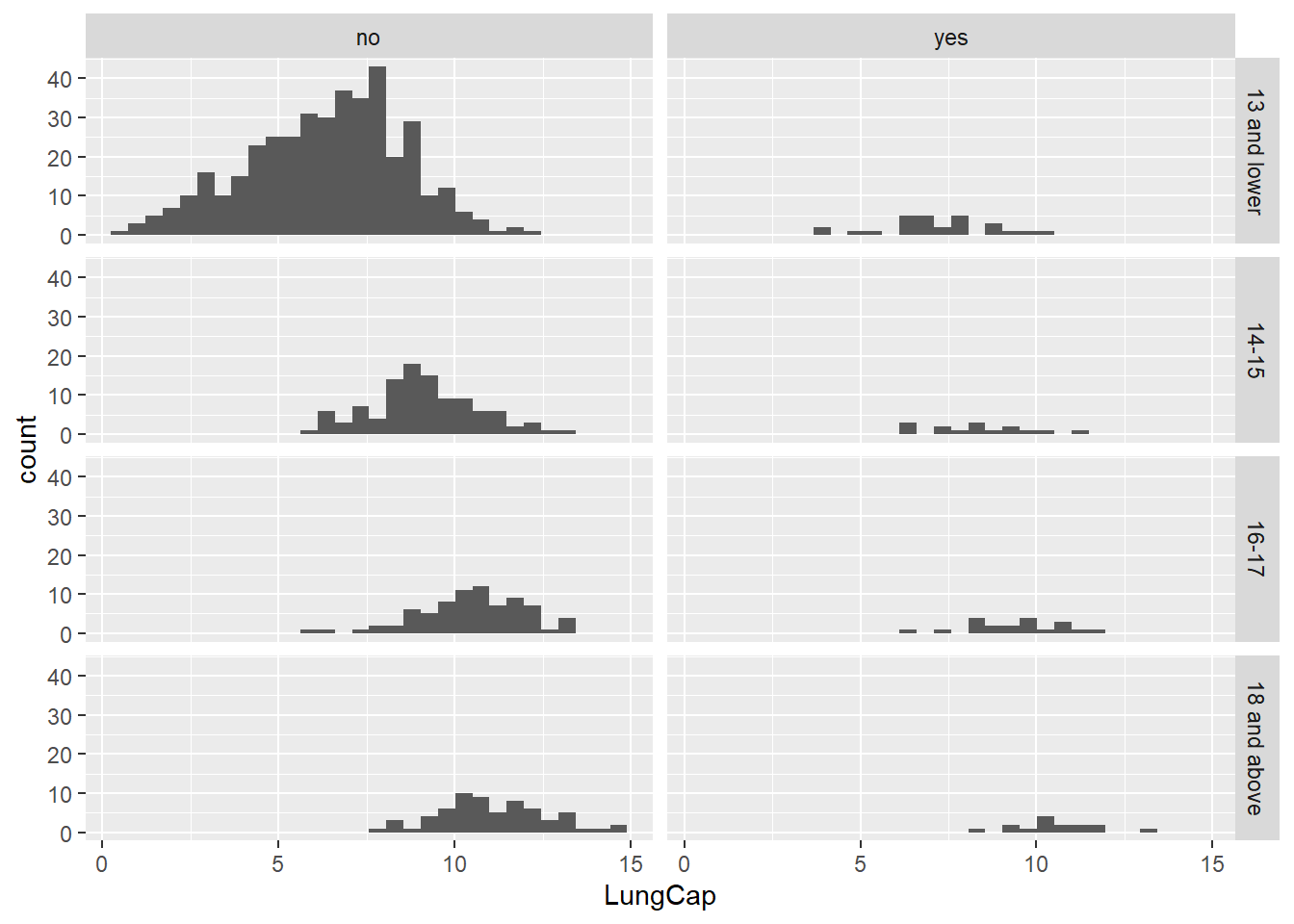
Majority seem to be non-smokers, and looks like non-smokers seem to have higher lung capacity.
`summarise()` has grouped output by 'AgeGroup'. You can override using the
`.groups` argument.# A tibble: 8 × 3
# Groups: AgeGroup [4]
AgeGroup Smoke `mean(LungCap)`
<fct> <chr> <dbl>
1 13 and lower no 6.36
2 13 and lower yes 7.20
3 14-15 no 9.14
4 14-15 yes 8.39
5 16-17 no 10.5
6 16-17 yes 9.38
7 18 and above no 11.1
8 18 and above yes 10.5 The mean lung capacity for smokers aged 13 and under is greater than that of non-smokers in the same age group which is different from expectation. Non-smokers have higher mean lung capacity for ages 14-15, 16-17 and 18 and above. Either there may be an error or extreme outlier in the data for smokers aged 13 and under.
Lung capacity and age have a high positive correlation of 0.82, meaning that as age increases, lung capacity also does. The covariance is a little more challenging to interpret; the positive number indicates a positive association between lung capacity and age, but because covariance varies from negative infinity to infinity, it is difficult to judge the strength of the relationship. In most situations, I would choose to employ correlation.
# A tibble: 5 × 3
df1 Inmate_count Probability
<int> <dbl> <dbl>
1 0 128 0.158
2 1 434 0.536
3 2 160 0.198
4 3 64 0.0790
5 4 24 0.0296The probability is about 19.75%.
The probability that a randomly selected inmate has fewer than 2 prior convictions is 0.6938272
The probability that a randomly selected inmate has 2 or fewer prior convictions is 0.891358.
The probability that a randomly selected inmate has more than 2 prior convictions is 0.108642.
The expected value for the number of prior convictions is 1.2864198. We can round this to 1.
The variance and the standard deviation for prior convictions are 0.8562353 and 0.9253298 respectively.
---
title: "Homework 1"
author: "Kaushika Potluri"
desription: "Something to describe what I did"
date: "08/02/2022"
format:
html:
toc: true
code-fold: true
code-copy: true
code-tools: true
categories:
- hw1
- challenge1
- my name
- dataset
- ggplot2
---
```{r}
#| label: setup
#| warning: false
knitr::opts_chunk$set(echo = TRUE)
```
### Loading in packages:
```{r}
library(readr)
library(ggplot2)
library(dplyr)
library(readxl)
```
### Reading in Data:
```{r}
df <- read_excel('_data/LungCapData.xls')
df
```
## 1(a) Distribution of LungCap:
```{r}
hist(df$LungCap)
```
The distribution appears to be very similar to a normal distribution, according to the histogram.
## 1(b)
The boxplots below show the probability distributions grouped by Gender.
```{r}
boxplot(LungCap~Gender, data=df)
```
Looks like males have a slightly higher lung capacity than females.
## 1 (c)
```{r}
df %>%
group_by(Smoke) %>%
summarize(Mean = mean(LungCap))
```
Surprisingly, the mean lung capacity is higher for smokers than it is for non-smokers.
## 1 (d)
```{r}
# convert Age to categorical variable.
df <- mutate(df, AgeGroup = case_when(Age <= 13 ~ "13 and lower", Age == 14 | Age == 15 ~ "14-15", Age == 16 | Age == 17 ~ "16-17", Age >= 18 ~ "18 and above"))
arrange(df, Age)
# construct histogram.
ggplot(df, aes(x = LungCap)) +
geom_histogram() +
facet_grid(AgeGroup~Smoke)
```
Majority seem to be non-smokers, and looks like non-smokers seem to have higher lung capacity.
## 1 (e)
```{r}
class(df$AgeGroup)
```
```{r}
df$AgeGroup <- as.factor(df$AgeGroup) #converting to factor
# construct table.
df %>% select(Smoke, LungCap, AgeGroup) %>% group_by(AgeGroup, Smoke) %>% summarise(mean(LungCap))
```
The mean lung capacity for smokers aged 13 and under is greater than that of non-smokers in the same age group which is different from expectation. Non-smokers have higher mean lung capacity for ages 14-15, 16-17 and 18 and above.
Either there may be an error or extreme outlier in the data for smokers aged 13 and under.
## 1 (f)
```{r}
cor(df$LungCap,df$Age)
```
```{r}
cov(df$LungCap,df$Age)
```
Lung capacity and age have a high positive correlation of 0.82, meaning that as age increases, lung capacity also does. The covariance is a little more challenging to interpret; the positive number indicates a positive association between lung capacity and age, but because covariance varies from negative infinity to infinity, it is difficult to judge the strength of the relationship. In most situations, I would choose to employ correlation.
## 2
```{r}
df1 <- c(0:4)
Inmate_count <- c(128, 434, 160, 64, 24)
IP<- data_frame(df1, Inmate_count)
```
## 2(a)
```{r}
IP <- mutate(IP, Probability = Inmate_count/sum(Inmate_count))
IP
```
```{r}
IP %>%
filter(df1 == 2) %>%
select(Probability)
```
The probability is about 19.75%.
## (b)
```{r}
df2 <- IP %>%
filter(df1 < 2)
sum(df2$Probability)
```
The probability that a randomly selected inmate has fewer than 2 prior convictions is 0.6938272
## 2(c)
```{r}
df3 <- IP %>%
filter(df1 <= 2)
sum(df3$Probability)
```
The probability that a randomly selected inmate has 2 or fewer prior convictions is 0.891358.
## 2(d)
```{r}
df4 <- IP %>%
filter(df1 > 2)
sum(df4$Probability)
```
The probability that a randomly selected inmate has more than 2 prior convictions is 0.108642.
## 2(e)
```{r}
IP <- mutate(IP, X = df1*Probability)
expectedvalue<- sum(IP$X)
expectedvalue
```
The expected value for the number of prior convictions is 1.2864198.
We can round this to 1.
## 2(f)
```{r}
var1 <-sum(((IP$df1-expectedvalue)^2)*IP$Probability)
var1
```
```{r}
sqrt(var1)
```
The variance and the standard deviation for prior convictions are 0.8562353 and 0.9253298 respectively.